Mi Diario Python

Introducción a las Redes Neuronales- Parte #1 - Tipos de Redes Neuronales

Luis Salcedo

31/07/2018 - Actualizado: 22/12/2020

Tipos de Redes Neuronales

Hemos visto la estructura de las redes neuronales, y sus conceptos básicos. Es hora de mencionar y desglosar los diferentes tipos de redes neuronales que nos toparemos al trabajar con estas.

Perceptrón Simple:

El modelo biológico más simple de un perceptrón es una neurona y viceversa. Es decir, el modelo matemático más simple de una neurona es un perceptrón. La neurona es una célula especializada y caracterizada por poseer una cantidad indefinida de canales de entrada llamados dendritas y un canal de salida llamado axón. Las dendritas operan como sensores que recogen información de la región donde se hallan y la derivan hacia el cuerpo de la neurona que reacciona mediante una sinapsis que envía una respuesta hacia el cerebro, esto en el caso de los seres vivos.

El perceptrón es una máquina de computación universal y tiene la expresividad equivalente a la lógica binaria ya que podemos crear un perceptrón que tenga el mismo comportamiento que una función booleana NAND y a partir de esta función se puede crear cualquier otra función booleana.

El perceptrón simple es una red que consta de dos capas de neuronas. 

Esta red admite valores binarios o bipolares como entrada para los sensores y los valores de su salida están en el mismo rango que los de entrada.
La función de la primera capa es hacer de sensor, por ella entran las señales a la red. 
La segunda capa realiza todo el procesamiento. La manera de interconexionar ambas capas es todas con todas esto es, cada neurona de la primera capa esta unida con todas las de la segunda capa.

Los pasos para que la red aprenda una lista de patrones son los siguientes

1 Tomar un patrón al azar de la lista.
2 Se establece el patrón de entrada en los sensores, la capa de entrada.
3 Se establecen los valores deseados en las neuronas de la capa de salida
4 Se actualizan las neuronas de la capa de Salida.
5 Solicitar que aprendan todas las sinapsis
6 Si las sinapsis han cambiado volver al paso 1
Si no han cambiado la red se ha estabilizado y paramos.

Las sinapsis que une las neuronas i, j aprenderá de la siguiente manera:

w = w + N * (d(k) - y) * x(k)

Donde:

W = El peso actual asociado a la sinapsis que une la neurona i de la capa de entrada y la neurona j de la capa de salida.
N = Es una constante entre 0 y 1 que indica cuanto aprende la red.
d(k) = El estado de la neurona de la capa de salida j.
y = El valor deseado para esa neurona.
x(k) = El estado de la neurona de la capa de entrada i.

El perceptrón simple tiene una serie de limitaciones, como lo es la incapazidad de clasificar conjuntos que no son linealmente independientes.

Por ello tenemos el Perceptrón Multicapa, y es aquí en donde nos topamos con otro tipo de red neuronal.

Perceptrón Multicapa

El perceptrón multicapa es una red neuronal artificial formada por múltiples capas, esto le permite resolver problemas que no son linealmente separables, lo cual es la principal limitación del perceptrón. El perceptrón multicapa puede ser totalmente o localmente conectado. En el primer caso cada salida de una neurona de la capa “i” es entrada de todas las neuronas de la capa “i+1”, mientras que en el segundo cada neurona de la capa “i” es entrada de una serie de neuronas (región) de la capa “i+1”.

Las capas pueden clasificarse en tres tipos:
§  Capa de entrada: Constituida por aquellas neuronas que introducen los patrones de entrada en la red. En estas neuronas no se produce procesamiento.
§  Capas ocultas: Formada por aquellas neuronas cuyas entradas provienen de capas anteriores y cuyas salidas pasan a neuronas de capas posteriores.
§  Capa de salida: Neuronas cuyos valores de salida se corresponden con las salidas de toda la red.

La propagación hacia atrás (también conocido como retropropagación del error o regla delta generalizada), es un algoritmo utilizado en el entrenamiento de estas redes, por ello, el perceptrón multicapa también es conocido como red de retropropagación.

Este modelo es una ampliación del perceptrón a la cual añade una serie de capas que, básicamente, hacen una transformación sobre las variables de entrada, que permiten eludir el problema de no clasificar conjuntos que no son linealmente independientes.

La Red de Hopfield

La red de Hopfield es una de las redes unicapas más importantes y ha influido en el desarrollo de multitud de redes posteriores.
Es una red autoasociativa no lineal que fue desarrollada por Hopfield en 1982 basándose en los modelos de redes de McCulloch y Pitts y los símiles de los campos magnéticos con spin de Amit, Gutfreund, & Sompolinsky.

Arquitectura de la red de hopfield

La red de Hopfield es una red monocapa, esto es, de una sola capa. Aunque también se puede mostrar como una red bicapa de dos capas, la primera capa seria una capa de sensores y la segunda capa será la capa donde se realiza el procesamiento.

En la versión bicapa la manera de interconexionar ambas capas es unir la primera capa a la segunda linealmente, esto es cada neurona con su respectiva, y después unir todas las neuronas con todas en la misma capa.

La red de Hopfield toma valores bipolares esto es, {-1,1}, sin embargo se pueden usar también valores binarios {0,1}.

Ejecutar un patrón en la red de Hopfield consiste en enviar un patrón en la red y actualizar las neuronas repetidamente hasta que se estabilicen los estados de las neuronas a un patrón memorizado.

Con pasos sería así.

1 Se establece el patrón de entrada en la capa de entrada.
2. Se actualizan las neuronas de la capa de procesamiento.
3. Si han cambiado el estado de la red o hemos realizada ya el número máximo de iteraciones paramos.
4. Si no volvemos al pasos 2.

Redes Competitivas

Las redes de aprendizaje competitivo se diferencian de las otras redes neuronales en que en las anteriores redes las neuronas colaboran en la representación de los patrones, sin embargo, en este tipo de redes cada neurona compite con las otras neuronas para representar los patrones.

El aprendizaje de este tipo de redes es como su nombre indica, competitivo.
Las neuronas compiten en cual representa mejor al patrón y la ganadora se lleva todo el aprendizaje de ese patrón. El objetivo de este tipo de redes es que se formen grupos de patrones, categorías, que son representados por cada neurona. 

Cuando ejecutamos un patrón en una red competitiva solamente se activa una neurona que es la que representa mejor el patrón.

Este tipo de redes fue desarrollado por Rumelhart y Zipser en 1985 aunque a partir de él se han diversificado sus aplicaciones y modificaciones dando lugar a redes tan interesantes como las redes de kohonen y otras.

Este es el ejemplo de red competitiva más simple que podemos encontrar ya que no introduce ninguna mejora.

Redes ART1

Las redes basadas en la teoría de resonancia adaptativa sirven para clasificar patrones de manera no supervisada, esto es, la red forma grupos y crea el número de categorías que crea conveniente en función de la configuración que le demos y las cualidades de los patrones.

Se considera que el aprendizaje no supervisado es el más posible desde un punto de vista psicológico, ya que los humanos aprendemos más sobre nuestra experiencia que escuchando a profesores. Un ejemplo de aprendizaje no supervisado es el siguiente: debemos clasificar una serie de objetos y no tenemos a nadie que nos diga a que categoría pertenece, así que tenemos que fijarnos en las características de los objetos y cuanto se parecen…

ART hace uso de dos términos usados en el estudio del comportamiento del celebro: Estabilidad y Plasticidad para llevar a cabo esta clasificación.
Estabilidad refleja la capacidad del sistema para recordar patrones previamente aprendidos. Plasticidad es la capacidad de aprender nuevos patrones

El equilibrio entre Estabilidad y Plasticidad es resuelto en las redes ART usando un parámetro llamado, granulidad , según algunos autores , otros lo llaman parámetro de vigilancia , yo he usado el anterior nombre por que expresa mejor la idea de una red con muchos categorías formando muchos y pequeños gránulos de patrones o formando pocos y grandes gránulos.

Este parámetro nos cuantifica cuanto debe diferenciarse un patrón al clasificar, del almacenado (estabilidad) en una categoría para que sea considerado una nueva categoría (plasticidad).

Redes ART2

La red ART2 es una ampliación de la red art1 que admite valores reales, como la anterior red, sirve para clasificar patrones de manera no supervisada

La arquitectura de la red ART2 es la misma que la de la art1. Consta de dos capas: la capa de entrada de sensores y la capa de salida, que en un principio no tiene ninguna neurona, pero que según vamos entrenando la red, esta va formando grupos de patrones que clasifica en una categoría cuyo patrón representativo son los pesos de entrada de la neurona de la capa de salida.

La manera de unirse ambas capas es total, cada neurona de la capa entrada esta unida con todas las neuronas de la capa de salida.

La diferencia principal entre la red art1 y la art2 es que esta última red admite valores reales.


Mapas de Kohonen. Redes Neuronales Autorganizativas.

La red de Kohonen pertenece a la categoría de redes no supervisadas, la diferencia con otras redes, es que las neuronas que representan patrones parecidos aparecen juntas en el espacio salida, este espacio puede ser unidimensional, una línea, bidimensional, un plano o N-dimensional. Es el propio diseñador de la red el que establece el espacio de salida que tendrá la red.

Las redes de kohonen son redes bicapas, esto es, de dos capas: la capa de entrada de sensores y la capa de salida que realiza el cálculo.

Cada neurona de la capa de salida debe reflejar las coordenadas que tiene en el espacio que el diseñador de la red decida. Para que las neuronas puedan ser comparadas con la posición de otras neuronas de la red, se le asocia una regla de vecindad.

El modo de unir las capas es todas con todas, total, cada neurona de la capa entrada esta unida con todas las neuronas de la capa de salida.

Referencias:

Luis Salcedo

  1. Vivasamcooke dice:
    abril 14, 2019 a las 8:04 am

    Estaría bien que incluyeseis un esquema de cada tipo de red, como para el perceptrón multicapa.

    Responder

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Introducción a las Redes Neuronales - Parte #1: Topologia de la Redes Neuronales

Luis Salcedo

24/07/2018 - Actualizado: 22/12/2020

1.4 Topología de las Redes Neuronales

La topogía o arquitectura de una rede neuronal consiste en la organización y disposición de las neuronas en la misma formando capas de neuronas alejadas de la entrada y salida de dicha red.

Los parámetros fundamentales de una red neuronal son: El número de capas, el número de neuronas por capa, el grado de conectividad y el tipo de conexión entre neuronas.

Por ello, repasaremos la topología y arquitectura de una red neuronal, clasificándolas por sus parámetros anteriormente mencionados.

1.4.1 Redes Monocapa 

Las redes monocapas, son aquellas que disponen de una sola capa. Este tipo de redes, utiliza conexiones laterales para conectarse con otras neuronas de su propia capa.
Este tipo de red son utilizadas generalmente para tareas de autoasociación.

Las redes monocapa más utilizadas son: 
  • la red de Hopfield
  • la red de BRAIN-STATE-IN-A-BOX
  • las maquinas estocasticas Botzmann y Cauchy.
  • Entre otros 
A continuación les mostrare una representación gráfica de una red monocapa:
Resultado de imagen para redes monocapa

1.4.2 Redes Multicapa:

Las redes multicapas son aquellas que disponen de un conjunto de neuronas
agrupadas en varios (2, 3, etc.) niveles o capas. En estos casos, una forma para
distinguir la capa a la que pertenece una neurona, consistiría en fijarse en el origen de
las señales que recibe a la entrada y el destino de la señal de salida. Normalmente,
todas las neuronas de una capa reciben señales de entrada desde otra capa anterior (la
cual está más cerca a la entrada de la red), y envían señales de salida a una capa
posterior (que está más cerca a la salida de la red). A estas conexiones se las denomina
conexiones hacia adelante o feedforward.

Sin embargo, en un gran número de estas redes también existe la posibilidad de
conectar la salida de las neuronas de capas posteriores a la entrada de capas anteriores;
a estas conexiones se las denomina conexiones hacia atrás o feedback.

Estas dos posibilidades permiten distinguir entre dos tipos de redes con
múltiples capas: las redes con conexiones hacia adelante o redes feedforward, y las
redes que disponen de conexiones tanto hacia adelante como hacia atrás o redes
feedforward/feedback.
Resultado de imagen para redes multicapa

1.4.3 Conexiones entre neuronas

La conectividad entre los nodos de una red neuronal está relacionada con la
forma en que las salidas de las neuronas están canalizadas para convertirse en entradas
de otras neuronas. La señal de salida de un nodo puede ser una entrada de otro elemento
de proceso, o incluso ser una entrada de sí mismo (conexión autorrecurrente).
Cuando ninguna salida de las neuronas es entrada de neuronas del mismo nivel o
de niveles precedentes, la red se describe como de conexión hacia delante Cuando las salidas pueden ser conectadas como entradas de neuronas de niveles
previos o del mismo nivel, incluyéndose ellas mismas, la red es de conexión hacia
atrás.
Las redes de propagación hacia atrás que tienen lazos cerrados son llamadas:
sistemas recurrentes.

1.4.4 Redes de propagación hacia atras (backpropagation)

El nombre de backpropagation resulta de la forma en que el error es propagado
hacia atrás a través de la red neuronal, en otras palabras el error se propaga hacia atrás
desde la capa de salida. Esto permite que los pesos sobre las conexiones de las neuronas
ubicadas en las capas ocultas cambien durante el entrenamiento.
El cambio de los pesos en las conexiones de las neuronas además de influir
sobre la entrada global, influye en la activación y por consiguiente en la salida de una
neurona. Por lo tanto, es de gran utilidad considerar las variaciones de la función
activación al modificarse el valor de los pesos. Esto se llama sensibilidad de la función
activación, de acuerdo al cambio en los pesos.
"Backpropagation" es un tema muy importante, y lo veremos más afondo, más adelante.

Luis Salcedo

  1. Diego dice:
    julio 25, 2018 a las 1:44 am

    Me gustan mucho tus publicaciones sobre Redes Neuronales. Esperare la próxima entrada.

    Responder
  2. Unknown dice:
    julio 25, 2018 a las 10:05 am

    Agradecerte tu publicación por hacer más cercano ese mundo "nuevo" y extraño que son las Redes Neuronales.

    Responder
  3. Unknown dice:
    julio 25, 2018 a las 4:15 pm

    HolA..!!! Como siempre...!!! muy bueno leer las publicaciones, aprender y sobretodo tambien difundir... En el Norte de Argentina tenemos un Grupo en Telegran @pythonnorte y alli posteo todas las publicaciones que generas...!! Gracias Luis...!! Te Seguimos..!!!

    Responder
  4. Alberto The Best dice:
    julio 26, 2018 a las 2:22 pm

    Deseando que hagas la siguiente publicación!!!

    Muchas gracias.

    Responder

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Introducción a las Redes Neuronales: Parte #1 - Métodos de Aprendizaje

Luis Salcedo

17/07/2018 - Actualizado: 22/12/2020

En este articulo nos centraremos en conocer los métodos de aprendizaje para el entrenamiento de las redes neuronales.


Como siempre, trata de explicarlo de manera clara  sencilla, sin tantas expresiones matemáticas. Claro, es inevitable tener que colocar más de 3 formulas, ya que es muy importante conocer los procesos matemáticos de las redes neuronales. Sabes que si tienes alguna duda, puedes dejar un comentario, y con gusto responderé.

Imagen relacionada

1.3 Métodos de Aprendizaje

Ya hemos vistos cual es la estructura de una red neuronal, vimos cuales eran sus capas y las funciones que realiza una neurona para recibir y transmitir información.

Las redes neuronales buscan imitar el proceso por el que pasa nuestro cerebro para aprender e interpretar los datos que se le den como entrada.

Igual que en el mundo físico, hay diferentes maneras en la que una red neuronal puede aprender. 

Una red neuronal debe aprender a calcular la salida correcta para un vector de entrada de un conjunto de ejemplos. Este proceso de aprendizaje los denominamos "proceso de entrenamiento o acondicionamiento". 

El aprendizaje de una red neuronal significa "adaptación de los pesos". Por lo tanto podemos decir que el aprendizaje es el proceso por el cual una red neuronal modifica sus pesos en respuesta a una información de entrada. Los cambios que se producen durante el mismo se reducen a la destrucción, modificación y creación de conexiones entre las neuronas. En los modelos de redes neuronales artificiales, la creación de una nueva conexión implica que el peso de la misma pasa a tener un valor distinto de cero. De la misma manera, una conexión se destruye cuando su peso pasa a ser cero.

Cuando la red neuronal esta en proceso de aprendizaje, los pesos de las conexiones de la red sufren modificaciones, por lo tanto, se puede afirmar que este proceso ha terminado (la red ha aprendido) cuando los valores de los pesos permanecen estables.
Una generalización de la fórmula o regla para decir los cambios en los pesos es
la siguiente:
Peso Nuevo = Peso Viejo + Cambio de Peso
Matemáticamente esto es:
wij(t+1) = wij(t) + Δwij(t)
donde t hace referencia a la etapa de aprendizaje, wij(t+1) al peso nuevo y wij(t) al peso
viejo.
Hay dos métodos de aprendizaje los cuales son los más importantes:
  • Aprendizaje Supervisado
  • Aprendizaje no supervisado

1.3.1 Aprendizaje Supervisado

El aprendizaje supervisado se caracteriza porque el proceso de aprendizaje se
realiza mediante un entrenamiento controlado por un agente externo (supervisor,
maestro) que determina la respuesta que debería generar la red a partir de una entrada
determinada. El supervisor controla la salida de la red y en caso de que ésta no coincida
con la deseada, se procederá a modificar los pesos de las conexiones, con el fin de
conseguir que la salida obtenida se aproxime a la deseada.
En este tipo de aprendizaje se suelen considerar, a su vez, tres formas de llevarlo
a cabo, que dan lugar a los siguientes aprendizajes supervisados:
  1. Aprendizaje por corrección de error
  2. Aprendizaje por refuerzo
  3. Aprendizaje estocástico

1.3.1.1 Aprendizaje por corrección de error 

Consiste en ajustar los pesos de las conexiones de la red en función de la
diferencia entre los valores deseados y los obtenidos a la salida de la red, es decir, en
función del error cometido en la salida.
Un ejemplo de este tipo de algoritmos lo constituye la regla de aprendizaje del
Perceptron, utilizada en el entrenamiento de la red del mismo nombre que desarrolló
Rosenblatt en 1958 [Rosenblatt 58]. Esta es una regla muy simple, para cada neurona en
la capa de salida se le calcula la desviación a la salida objetivo como el error, δ. El cual
luego se utiliza para cambiar los pesos sobre la conexión de la neurona precedente. El
cambio de los pesos por medio de la regla de aprendizaje del Perceptron se realiza
según la siguiente regla:
Δwij = σ*outj*(aqi – outi);
donde: aqi es la salida deseada/objetivo de la neurona de salida Ni, δi = (aqi – outi) la
desviación objetivo de la neurona Ni y σ el aprendizaje.
La salida de la neurona Nj (outj) se utiliza, porque este valor influye en la entrada
global y, por ende, en la activación y luego en la salida de la neurona Ni. Esto es
semejante a un “efecto en cadena”.
Otro algoritmo muy conocido y que pertenece a esta clasificación es la regla de
aprendizaje Delta o regla del mínimo error cuadrado (LMS Error: Least Mean Squared
Error), que también utiliza la desviación a la salida objetivo, pero toma en consideración
a todas las neuronas predecesoras que tiene la neurona de salida. Esto permite
cuantificar el error global cometido en cualquier momento durante el proceso de
entrenamiento de la red, lo cual es importante, ya que cuanto más información se tenga
sobre el error cometido, más rápido se puede aprender. Luego el error calculado (δ) es
igualmente repartido entre las conexiones de las neuronas predecesoras.
Por último se debe mencionar la regla de aprendizaje de propagación hacia
atrás o de backpropagation, también conocido como regla LMS multicapa, la cual es
una generalización de la regla de aprendizaje Delta. Esta es la primer regla de
aprendizaje que permitió realizar cambios sobre los pesos en las conexiones de la capa
oculta.

1.3.1.2 Aprendizaje por refuerzo

Se trata de un aprendizaje supervisado, más lento que el anterior, que se basa en
la idea de no disponer de un ejemplo completo del comportamiento deseado, es decir, de
no indicar durante el entrenamiento exactamente la salida que se desea que proporcione
la red ante una determinada entrada.
En el aprendizaje por refuerzo la función del supervisor se reduce a indicar
mediante una señal de refuerzo si la salida obtenida en la red se ajusta a la deseada
(éxito = +1 o fracaso = -1), y en función de ello se ajustan los pesos basándose en un
mecanismo de probabilidades. Se podría decir que en este tipo de aprendizaje la función
del supervisor se asemeja más a la de un crítico (que opina sobre la respuesta de la red)
que a la de un maestro (que indica a la red la respuesta concreta que debe generar),
como ocurría en el caso de supervisión por corrección del error.

1.3.1.3 Aprendizaje estocástico

Consiste básicamente en realizar cambios aleatorios en los valores de los pesos
de las conexiones de la red y evaluar su efecto a partir del objetivo deseado y de
distribuciones de probabilidad.
En el aprendizaje estocástico se suele hacer una analogía en términos
termodinámicos, asociando a la red neuronal con un sólido físico que tiene cierto estado
energético. En el caso de la red, la energía de la misma representaría el grado de
estabilidad de la red, de tal forma que el estado de mínima energía correspondería a una
situación en la que los pesos de las conexiones consiguen que su funcionamiento sea el
que más se ajusta al objetivo deseado.
Según lo anterior, el aprendizaje consistiría en realizar un cambio aleatorio de
los valores de los pesos y determinar la energía de la red (habitualmente la función
energía es una función de Liapunov). Si la energía es menor después del cambio, es
decir, si el comportamiento de la red se acerca al deseado, se acepta el cambio; si, por el
contrario, la energía no es menor, se aceptaría el cambio en función de una determinada
y preestablecida distribución de probabilidades.

1.3.2 Aprendizaje no supervisado

Las redes con aprendizaje no supervisado (también conocido como
autosupervisado) no requieren influencia externa para ajustar los pesos de las
conexiones entre sus neuronas. La red no recibe ninguna información por parte del
entorno que le indique si la salida generada en respuesta a una determinada entrada es o
no correcta.
Estas redes deben encontrar las características, regularidades, correlaciones o
categorías que se puedan establecer entre los datos que se presenten en su entrada.
Existen varias posibilidades en cuanto a la interpretación de la salida de estas redes, que
dependen de su estructura y del algoritmo de aprendizaje empleado.
En algunos casos, la salida representa el grado de familiaridad o similitud entre
la información que se le está presentando en la entrada y las informaciones que se le han
mostrado hasta entonces (en el pasado). En otro caso, podría realizar una clusterización
(clustering) o establecimiento de categorías, indicando la red a la salida a qué categoría
pertenece la información presentada a la entrada, siendo la propia red quien debe
encontrar las categorías apropiadas a partir de las correlaciones entre las informaciones
presentadas.
En cuanto a los algoritmos de aprendizaje no supervisado, en general se suelen
considerar dos tipos, que dan lugar a los siguientes aprendizajes:
  1. Aprendizaje hebbiano.
  2. Aprendizaje competitivo y comparativo.

1.3.1.1 Aprendizaje hebbiano

Esta regla de aprendizaje es la base de muchas otras, la cual pretende medir la
familiaridad o extraer características de los datos de entrada. El fundamento es una
suposición bastante simple: si dos neuronas Ni y Nj toman el mismo estado
simultáneamente (ambas activas o ambas inactivas), el peso de la conexión entre ambas
se incrementa.
Las entradas y salidas permitidas a la neurona son: {-1, 1} o {0, 1} (neuronas
binarias). Esto puede explicarse porque la regla de aprendizaje de Hebb se originó a
partir de la neurona biológica clásica, que solamente puede tener dos estados: activa o
inactiva.

1.3.1.2 Aprendizaje competitivo y comparativo

Se orienta a la clusterización o clasificación de los datos de entrada. Como
característica principal del aprendizaje competitivo se puede decir que, si un patrón
nuevo se determina que pertenece a una clase reconocida previamente, entonces la
inclusión de este nuevo patrón a esta clase matizará la representación de la misma. Si el
patrón de entrada se determinó que no pertenece a ninguna de las clases reconocidas
anteriormente, entonces la estructura y los pesos de la red neuronal serán ajustados para
reconocer la nueva clase.

Luis Salcedo

  1. Unknown dice:
    julio 21, 2018 a las 2:10 pm

    Umm. Lo leere mas tarde con calma. Podrías hacer según esto un mayordomo o algo así?. Ejemplo alguien virtual que responda cosas coherentes en una sala de chat?
    Y que aprenda de las preguntas que se le hagan.? Umm eso es inteligencia Artificial. Plis muestrenme un pequeño código en python que haga algo parecido ...

    Responder
    1. Luis Salcedo dice:
      julio 24, 2018 a las 5:53 pm

      Hola. Por supuesto, nada es imposible. Claro, para crear un bot capaz de interpretar las preguntas y puede retornar respuestas coherentes, es un complicado ya implica muchos procesos incluyendo procesamiento del lenguaje natural que es otro tema amplio, en un futuro espero poder realizar un proyecto como ese y compartirlo. Pero si necesitas un bot como el que describes, te recomiendo https://dialogflow.com/ es una API mantenida por Google, es muy buena te la recomiendo, tienen implementaciones en diversos lenguajes (incluyendo python) también lo puedes integrar a Telegram, Facebook Messdenger, Google Assistant y mucho más.

      Responder
  2. Unknown dice:
    agosto 7, 2018 a las 2:10 am

    Me encanta que alguien este investigando y realizar una red neural con python te doy mi apoyo esa idea de crear un cerebro virtual que pueda pensar estubo en mis ideas hace ya 2 años pero sigo estudiado un poco mas de lo que ya se.

    Responder

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Introducción a las Redes Neuronales - Parte #1: Elementos básicos de una Red Neuronal

Luis Salcedo

13/07/2018 - Actualizado: 22/12/2020

Segundo capitulo de la guía "introducción a las Redes Neuronales". En este capitulo 1.2 de la parte #1, veremos cuales son los elementos básicos que componen a una Red Neuronal.

1.2 Elementos básicos de una Red Neuronal


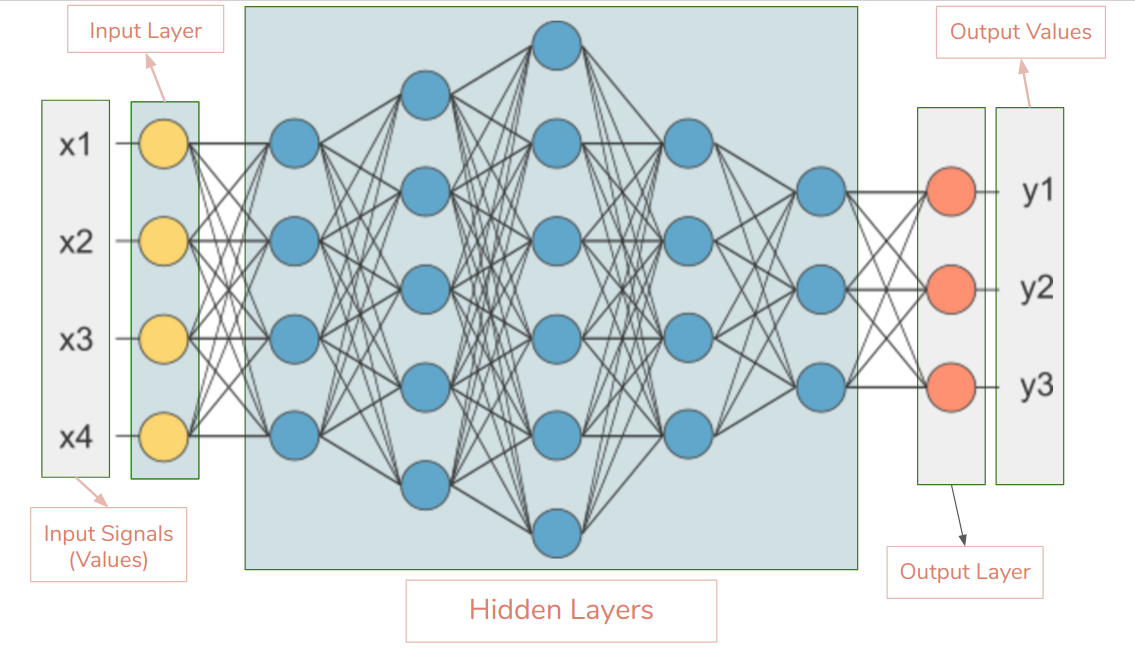
Las redes neuronales están interconectadas por 3 capas. La primera es la capa de entrada, la segunda son las capas ocultas, y por ultimo la capa de salida. Es importante saber, que las capas ocultas pueden estar constituidas por todas las capas que sean necesarias. Hay redes neuronales que utilizan cientos de capas ocultas. Claro, es un proceso más costoso, pero veremos cuales son los beneficios de esto más adelante.


Ahora les describiré las funciones que determinan una neurona y su proceso: función de entrada, función de activación y la función de salida.

Función de entrada:

La neurona trata a muchos valores de entrada como si fueran uno solo; esto
recibe el nombre de entrada global. Esto nos genera un problema, como vamos a combinar todas estas simples entradas (ini1, ini2, ...) dentro de la entrada global (gin)?

Esto lo lograremos a través de la función de entrada, la cual se calcula a partir del vector entrada. La función de entrada puede describirse matemáticamente de la siguiente manera:

donde: * representa al operador apropiado (por ejemplo: máximo, sumatoria,
productoria, etc.), n al número de entradas a la neurona Ni y wi al peso.

Los valores de entrada se multiplican por los pesos anteriormente ingresados a la
neurona. Por consiguiente, los pesos que generalmente no están restringidos cambian la
medida de influencia que tienen los valores de entrada. Es decir, que permiten que un
gran valor de entrada tenga solamente una pequeña influencia, si estos son lo
suficientemente pequeños. 

Resultado de imagen para redes neuronales

En la imagen anterior podemos ver los elementos de una red neuronal. x = vector de entrada, x1 = entrada número
1 a la neurona; w(1) = peso correspondiente a x1; x2 = entrada número 2 a la
neurona; w(2) = peso correspondiente a x2; y Y = salida de la neurona Ni. El
conjunto de todas las n entradas ini = (ini1, ini2, ..., inin) es comúnmente llamado “vector
entrada”.

Algunas de las funciones de entrada más comúnmente utilizadas y conocidas
son: 

1) Sumatoria de las entradas pesadas: es la suma de todos los valores de
entrada a la neurona, multiplicados por sus correspondientes pesos.


2) Productoria de las entradas pesadas: es el producto de todos los valores de
entrada a la neurona, multiplicados por sus correspondientes pesos.

3) Máximo de las entradas pesadas: solamente toma en consideración el valor
de entrada más fuerte, previamente multiplicado por su peso correspondiente.

Función de Activación

La función de activación calcula el estado de una neuronal; transformando la entrada global en un valor de activación, cuyo rango normalmente va de "0 a 1" o de "-1 a 0". El valor sera "0 o -1" para las neuronas inactivas y "1" para las neuronas activas.

La función activación, es una función de la entrada global (gini) menos el umbral
(Θi). A continuación describiré las 3 funciones de activación más comunes.

1) Función Lineal:

Los valores de salida obtenidos por
medio de esta función de activación serán:
a·(gini - Θi), cuando el argumento de (gini - Θi)
esté comprendido dentro del rango (-1/a, 1/a).
Por encima o por debajo de esta zona se fija la salida en 1 o –1, respectivamente.  

Básicamente la función de activación se puede describir de la siguiente manera:

t(x) = 0  si x< T

t(x) = 1  si x≥ T

Donde  T  es el nivel de activación elegido.

2) Función sigmoide:
Los valores de salida que
proporciona esta función están comprendidos
dentro de un rango que va de 0 a 1. Al
modificar el valor de g se ve afectada la
pendiente de la función de activación. 
3) Función Tangente hiperbólica
Los valores de salida de la función
tangente hiperbólica están comprendidos dentro de
un rango que va de -1 a 1. Al modificar el valor de g
se ve afectada la pendiente de la función de
activación. 

¿Por que es importante saber si una neurona esta activada o no? Si una neurona esta activada, pasara los datos que recibe a la siguiente neurona de la siguiente capa, de lo contrario, esta no enviara ningún tipo de información.

De hecho es muy parecido al proceso biológico de nuestras neuronas. Las neuronas pueden estar activadas (excitadas) o inactivas (No excitadas).

3) Función de salida
Por ultimo, tenemos a la función de salida. Esta función devuelve la salida de la neurona, por lo que la función de salida determina el valor que se transfiere a las neuronas vinculadas. Si la función de
activación está por debajo de un umbral determinado, ninguna salida se pasa a la
neurona subsiguiente. Normalmente, no cualquier valor es permitido como una entrada
para una neurona, por lo tanto, los valores de salida están comprendidos en el rango
[0, 1] o [-1, 1]. También pueden ser binarios {0, 1} o {-1, 1}. 

Dos de las funciones de salida más comunes son:  
  • Ninguna: este es el tipo de función más sencillo, tal que la salida es la misma
    que la entrada. Es también llamada función identidad.
  •  Binaria: {0,1}


Hasta aquí llegaremos hoy. Se que es un tema un poco complicado de entender. Así que si tienes dudas, las responderé con mucho gusto.

Mi nombre es Luis, y fue un placer compartir mis conocimientos con todos ustedes :D.

Luis Salcedo

  1. Anónimo dice:
    julio 14, 2018 a las 5:07 am

    que bien espero la próxima publicación

    Responder
  2. Anónimo dice:
    julio 15, 2018 a las 11:09 pm

    A la espera del próximo artículo. Hace tiempo esperaba algo así. Estaba estudiando redes neuronales en un par de libros, aunque artículos así es lo mejor por su sencillez que, sin embargo, no dejan de lado conceptos importantes. Sigo el blog de hace unos 6 meses, y a verdad es que hacen un gran trabajo en cada artículo publicado. Sigan así. Muchas gracias!!

    Responder
  3. Unknown dice:
    julio 16, 2018 a las 1:04 pm

    Sencillo, y muy provechoso el artículo

    Responder
  4. Diego dice:
    julio 25, 2018 a las 12:53 am

    Continuaré la lectura.

    Responder
  5. Unknown dice:
    julio 31, 2018 a las 2:33 am

    Gracias Luis, me pareció importante y pertinente para mi proyecto.

    Responder

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Introducción a las Redes Neuronales - Parte #1: ¿Qué es una Red Neuronal?

Luis Salcedo

11/07/2018 - Actualizado: 22/12/2020

Este articulo es la apertura a la guía de "Introducción a las redes neuronales", tema que eligieron nuestro usuarios en una encuesta realizada hace algunos días.


En este articulo les explicare como sera la estructura de la guía. Y veremos la primera parte de la guía "1.1 ¿Que es una Red Neuronal?".

Introducción:

A lo largo de los años, el área de la inteligencia artificial ha evolucionado de manera exponencial. Siempre que escuchamos esta palabra, "Inteligencia Artificial", nos imaginamos muchos escenarios, ya sea un robot que viaja al pasado a matar a Sarah Connor, o una maquina capaz de realizar un proceso de reconocimiento facial.
¿Que es en lo que piensas al escuchar: "Inteligencia Artificial"?.

Robots y maquinas que pueden ver. Al decirlo puede parecer algo muy difícil de entender y de hacer. Imaginamos que es algo que solo genios pueden lograr.

Pero como sucede con campos de las matemáticas y con la programación, muchos lo ven como algo casi imposible de entender. Pero no es así. Solo debemos saber que información es la correcta digerir, y cuales son los pasos para comenzar en esa área.

Por ello, he realizado este curso, tutorial, guía, como lo quieras ver. En el, plasmare toda mi experiencia y conocimientos sobre las "Redes Neuronales", el pilar fundamental de la "Inteligencia Artificial".

Veremos todo los conceptos y la teoría necesaria para entender el funcionamiento de una red neuronal artificial.

Luego, con ayuda de todo lo aprendido, construiremos nuestras propias redes neuronales implementándolas en el lenguaje de programación Python.

Pienso en dividir el docuemnto en 2 partes:
  • Parte #1 - No hay practica sin teoría: En toda esta parte, veremos toda la teoria y los conceptos necesarios para conocer el proceso de las redes neuronales, sus caracteristicas, sus tipos, y todo los lo que sea necesario conocer.
  • Parte #2 - La practica hace al maestro: En  esta parte, pondremos a prueba todos lo aprendido. Practicaremos los más que podamos. Construiremos nuestras propias redes y les daremos problemas del mundo real.

Espero que puedas disfrutar de este contenido. Es la primera vez que realizo un proyecto de enseñanza como este. Así que si cometo errores, por favor, no sean tan duros conmigo.

Mi nombre es Luis, y te deseo una muy buena lectura.

Índice
  • Parte #1 - No hay practica sin teoría

    • Parte #1 - No hay practica sin teoría

    1.1 ¿Qué es una Red Neuronal?

    La unidad básica del sistema nervioso, es la neurona. Las neuronas se encargan de recibir información (atrevas del axon) y de enviar información a otras neuronas a través de las dendritas. 

    Las redes neuroanles artificiales, igual que los cerebros reales, se forman a partir de "neuronas" conectadas, todas capaces de llevar a cabo una tarea relacionada con los datos. Por ejemplo, el reconocimiento de patrones.

    Como mencione anteriormente, las neuronas reciben y envían información. En una red neuronal, cada neurona transmite su trabaja a una neurona vecina, que luego podrá procesarla y enviarla a otra neurona. Esto proceso, muy parecido a el que realiza el de nuestro cerebro.

    Las redes neuronales se organizan en capas. Las diferentes capas pueden realizar diferentes tipos de procesamientos en los datos de entrada. Las entradas viajan desde la primera capa (entrada) hasta la ultima capa (salida), antes de haber pasado por varias capas (ocultas) que realizan un procesamiento muy interno. Todo esto producirá una salida.

    Resultado de imagen para red neuronal simple
    Figura 1.1. Red neuronal simple.
    Debido a que la red es capaz de cambiar y adaptarse en función de los datos que pasan a través de ella, las conexiones entre estas neuronas se ajustan hasta que la red genera predicciones altamente precisas. Este proceso es muy parecido a la manera en la que nuestro cerebro aprende.

    Las redes neuronales se utilizan en una gran variedad de tareas:
    • Visión Artificial
    • Reconocimiento de voz
    • Tablero de juegos y videojuegos
    • Traducción automactica
    • Diagnósticos médicos
    • Procesamiento del lenguaje natural
    • Clasificación de correo basura
    • Clasificación de imágenes
    • Creación de Chatbots
    • Reconocimiento óptico de caracteres
    • Y mucho más.
    ¿Alguna duda? ¿Crees que hace falta información? Por favor déjanos tu comentario.

    Luis Salcedo

    1. Unknown dice:
      julio 12, 2018 a las 3:27 pm

      intersante, quiero mas...

      Responder
    2. Luis Salcedo dice:
      julio 12, 2018 a las 7:28 pm

      Hola. Por supuesto, hay más de donde salio este. En el próximo veremos cual es el procedimiento utilizado para entrenar a una red neuronal.

      Saludos.

      Responder
    3. Fernando Miño dice:
      julio 13, 2018 a las 1:37 am

      Bueno nos dejas con la expectativa y a la espera, gracias.

      Responder
    4. Diego dice:
      julio 25, 2018 a las 12:38 am

      Estoy siguiendo esta serie porque estoy leyendo sobre redes neuronales. Muy interesante. Gracias por tu trabajo.

      Responder
    5. Unknown dice:
      agosto 2, 2018 a las 4:31 pm

      Gracias siga así

      Responder
    6. Unknown dice:
      agosto 7, 2018 a las 4:44 pm

      Excelente aporte, esperamos mucho más sobre este tema, saludos cordiales.

      Responder

    Deja una respuesta

    Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

    Subir
    White Monkey