Árbol binario de búsqueda - Estructura de datos en Python
Introducción:
Hola amigos de Internet, mi nombre es Luis, y les doy nuevamente la bienvenida a "Mi Diario Python", el mejor blog hispanoamericano para Aprender Python.
En el día de hoy veremos un tema de estudio universitario muy importante en el área de ciencias de la computación, Árboles binario. Más específicamente, hablaremos sobre Árboles binario de búsqueda.
Al final, como siempre, realizaremos una implementación en Python.
Árbol Binario:
Un árbol binario es un conjunto de elementos cada uno de los cuales de denomina nodo. Si un nodo no contiene datos, se dice que es un nodo externo, de lo contrario lo denominamos nodo interno.
Un árbol binario es una estructura de dato no lineal en la que cada nodo puede apuntar a uno o máximo dos nodos, por ello el nombre "binario".
La imagen anterior representa un árbol binario de tamaño 9, 3 niveles, y altura 3 con un nodo raíz cuyo valor es 2.
Los árboles binarios son considerados como estructuras de datos jerárquicas y como tal su forma de recorrerlos difiere sustancialmente.El recorrido de un árbol binario se lleva a cabo en tres sentidos: Preorden, Inorden y Postorden.
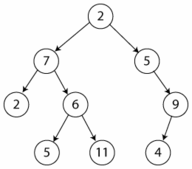
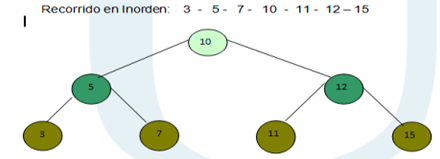
Recorrido en Preorden:
El recorrido en preorden consiste, en primer lugar, en examinar el dato del nodo raíz, posteriormente se recorre el subárbol derecho en preorden y luego el subárbol izquierdo en preorden.
A continuación te mostrare una image con un árbol binario cuyo recorrido es en preorden:
El recorrido inicia con el subárbol izquierdo, el primer nodo a visitar es la raíz que es el nodo 10, luego se visita el subárbol izquierdo con el nodo 5, posteriormente el 3, luego el nodo 1, sigue con el nodo 4, pasamos al nodo 7 y luego el 9.
Continuamos con el recorrido del subárbol derecho en preorden, con la visita del nodo 15, luego el 14, se continúa con el 17, se visita el 16 y se finaliza con la visita del nodo 20.
Recorrido en Inorden:
El recorrido en Inorden consiste en recorrer el subárbol izquierdo en Inorden, luego se examina el dato del nodo raíz, y finalmente se recorre el subárbol derecho en Inorden.
El recorrido inicia con el subárbol izquierdo, el primer nodo a visitar es el 3 luego se visita el 5 y posteriormente el 7, con esto se garantiza que el recorrido del subárbol izquierdo se hizo en Inorden.
Finalizado el recorrido del subárbol izquierdo se visita el nodo de la raíz, que para este caso es el numero 10.
Solo queda recorrer el subárbol derecho en Inorden, es decir se visita el 11 luego el 12 y se finaliza con la visita del nodo 15.
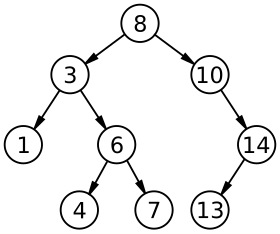
Recorrido en Posorden:
El recorrido en postorden consiste en recorrer el subárbol izquierdo en postorden, luego el subárbol derecho en postorden, y finalmente examinar el dato del nodo raíz.
El recorrido inicia con el subárbol izquierdo, el primer nodo a visitar es el 3 luego se visita el 7 y posteriormente el 5 que es la raíz, con esto se garantiza que el recorrido del subárbol izquierdo se hizo en Postorden.
Finalizado el recorrido del subárbol izquierdo se inicia la visita al subárbol derecho en Postorden, es decir, se visita el 11 luego el 15 y se finaliza con la visita del nodo 12 que sería la raíz de este subárbol.
Solo queda recorrer la raíz del árbol que para este caso es el número 10.
Árbol binario de búsqueda:
Los árboles binarios de búsqueda, son un tipo especial de árbol binario cuya característica radica en la forma ordenada de insertar sus elementos, facilitando así la búsqueda de un nodo en particular.
La forma en la que se ordenan los nodos es la siguiente:
- la rama de la izquierda contendrá elementos menores
- la rama de la derecha contendrá elementos mayores
Las operaciones de un árbol binario de búsqueda son las siguientes:
- Búsqueda: consiste en acceder a la raíz del árbol si el elemento a localizar coincide con éste la búsqueda ha concluido con éxito, si el elemento es menor se busca en el subárbol izquierdo y si es mayor en el derecho.
- Inserción: es muy similar a la búsqueda y se puede dar una solución tanto iterativa como recursiva. Si tenemos inicialmente como parámetro un árbol vacío se crea un nuevo nodo como único el elemento a insertar. Si no lo está, se comprueba si el elemento dado es menor que la raíz.
- Borrado: La operación de borrado se puede realizar de tres formas diferentes. Borrar un nodo sin hijos o nodo hoja, Borrar un nodo con su subárbol hijo y Borrar un nodo con dos subárboles hijo.
- Recorridos: ya repasamos los recorridos de un árbol binario. Veamos otro ejemplo:
Inorden = [6, 9, 13, 14, 15, 17, 20, 26, 64, 72].
Preorden = [15, 9, 6, 14, 13, 20, 17, 64, 26, 72].
Postorden =[6, 13, 14, 9, 17, 26, 72, 64, 20, 15].
Implementación:
Ahora, pongamos a prueba todo lo aprendido. Realizaremos todos los procesos mencionados anteriormente, crearemos un árbol binario de búsqueda con todas sus operaciones y su respectivo recorrido:
Puedes descargar y visualizar el código ingresando al siguiente enlace:
from __future__ import print_function # Declaramos la clase "Node" class Node: def __init__(self, label, parent): self.label = label self.left = None self.right = None self.parent = parent # Métodos para asignar nodos def getLabel(self): return self.label def setLabel(self, label): self.label = label def getLeft(self): return self.left def setLeft(self, left): self.left = left def getRight(self): return self.right def setRight(self, right): self.right = right def getParent(self): return self.parent def setParent(self, parent): self.parent = parent class BinarySearchTree: def __init__(self): self.root = None def insert(self, label): # Creamos un nuevo nodo new_node = Node(label, None) # Si el árbol esta vacio if self.empty(): self.root = new_node else: # Si el árbol no esta vacio curr_node = self.root while curr_node is not None: parent_node = curr_node if new_node.getLabel() < curr_node.getLabel(): curr_node = curr_node.getLeft() else: curr_node = curr_node.getRight() if new_node.getLabel() < parent_node.getLabel(): parent_node.setLeft(new_node) else: parent_node.setRight(new_node) new_node.setParent(parent_node) # Operación de borrado def delete(self, label): if (not self.empty()): node = self.getNode(label) if(node is not None): if(node.getLeft() is None and node.getRight() is None): self.__reassignNodes(node, None) node = None elif(node.getLeft() is None and node.getRight() is not None): self.__reassignNodes(node, node.getRight()) elif(node.getLeft() is not None and node.getRight() is None): self.__reassignNodes(node, node.getLeft()) else: tmpNode = self.getMax(node.getLeft()) self.delete(tmpNode.getLabel()) node.setLabel(tmpNode.getLabel()) def getNode(self, label): curr_node = None if(not self.empty()): curr_node = self.getRoot() while curr_node is not None and curr_node.getLabel() is not label: if label < curr_node.getLabel(): curr_node = curr_node.getLeft() else: curr_node = curr_node.getRight() return curr_node def getMax(self, root = None): if(root is not None): curr_node = root else: curr_node = self.getRoot() if(not self.empty()): while(curr_node.getRight() is not None): curr_node = curr_node.getRight() return curr_node def getMin(self, root = None): if(root is not None): curr_node = root else: curr_node = self.getRoot() if(not self.empty()): curr_node = self.getRoot() while(curr_node.getLeft() is not None): curr_node = curr_node.getLeft() return curr_node def empty(self): if self.root is None: return True return False def __InOrderTraversal(self, curr_node): nodeList = [] if curr_node is not None: nodeList.insert(0, curr_node) nodeList = nodeList + self.__InOrderTraversal(curr_node.getLeft()) nodeList = nodeList + self.__InOrderTraversal(curr_node.getRight()) return nodeList def getRoot(self): return self.root def __isRightChildren(self, node): if(node == node.getParent().getRight()): return True return False def __reassignNodes(self, node, newChildren): if(newChildren is not None): newChildren.setParent(node.getParent()) if(node.getParent() is not None): if(self.__isRightChildren(node)): node.getParent().setRight(newChildren) else: node.getParent().setLeft(newChildren) def traversalTree(self, traversalFunction = None, root = None): if(traversalFunction is None): return self.__InOrderTraversal(self.root) else: return traversalFunction(self.root) def __str__(self): list = self.__InOrderTraversal(self.root) str = "" for x in list: str = str + " " + x.getLabel().__str__() return str def InPreOrder(curr_node): nodeList = [] if curr_node is not None: nodeList = nodeList + InPreOrder(curr_node.getLeft()) nodeList.insert(0, curr_node.getLabel()) nodeList = nodeList + InPreOrder(curr_node.getRight()) return nodeList # Función para probar las clases def testBinarySearchTree(): ''' Ejemplo 8 / 3 10 / 1 6 14 / / 4 7 13 ''' ''' Ejemplo luego del borrado 7 / 1 4 ''' # Instancia del árbol binario de búsqueda t = BinarySearchTree() #Insertamos los elementos t.insert(8) t.insert(3) t.insert(6) t.insert(1) t.insert(10) t.insert(14) t.insert(13) t.insert(4) t.insert(7) print(t.__str__()) if(t.getNode(6) is not None): print("El elemento 6 existe") else: print("El elemento 6 no existe") if(t.getNode(-1) is not None): print("El elemento -1 existe") else: print("El elemento -1 no existe") if(not t.empty()): print(("Valor Max: ", t.getMax().getLabel())) print(("Valor Min: ", t.getMin().getLabel())) t.delete(13) t.delete(10) t.delete(8) t.delete(3) t.delete(6) t.delete(14) # Obtenemos todos los elementos del árbol en preorden list = t.traversalTree(InPreOrder, t.root) for x in list: print(x) if __name__ == "__main__": testBinarySearchTree()
8 3 1 6 4 7 10 14 13
El elemento 6 existe
El elemento -1 no existe
('Valor Max: ', 14)
('Valor Min: ', 1)
7
1
4
Como pueden observar, el resultado es satisfactorio. Nos muestra el árbol. Lo elementos los cuales solicitamos su estado de existencia. El valor más alto y el más bajo. Y el árbol luego de eliminar algunos nodos.
Estructura de datos es un tema muy interesante e importante, por ello tratare de darle más espacio en el blog.
¿Alguna duda? ¿Alguna sugerencia? Deja tu comentario.
Mi nombre es Luis, y fue un placer compartir mis conocimientos con todos ustedes :D.
-
-
Unknown dice: Excelente publicación, me gustaría hacer un programa en python que de una lista de datos creciente.. Empezando por 100 detectara patrones de comportamiento. Ejemplo se introduce el nombre Javier y siempre que aparece aparece luego del nombre el de Pedro..
Creo que en números es mas fácil .. En una lista siempre que aparece el # 5 le sigue el 50 entonces patrón repetitivo 5-50, me ayudas a hacer algo así-
Luis Salcedo dice:
Sí, efectivamente, te recomiendo pasarle a los nombres un numero con el cual identificarlo, luego hacer que la neurona los procese.
-
-
-
Mari Carmen dice:
Hola, necesitaría ayuda. Tengo unos datos que conforman un árbol no binario. Estos están en dos columnas (inicio,fin), de manera que si iniciamos en la raíz(por ejemplo está en la columna fin), el elemento descendiente será el que está en la misma posición que la raíz pero en la otra columna inicio. Luego este mismo descendiente lo encontraremos en la columna fin, i su descendiente será el elemento que se encuentra en la columna inicio, de nuevo. y así sucesivamente. Después cuando hay ramificaciones, el nodo desde donde salen las ramificaciones se repetirá tantas veces como descendientes haya.
Mi pregunta es, es posible con estos datos, utilizar el algoritmo que has propuesto? Si es así, me podrías dar algunas nociones de como hacerlo?
Muchas gracias de antemano, hace tiempo que estoy encallada, buscando una manera óptima de crear el árbol/red.PD: no sé si me expliqué bien
-
Unknown dice:
Hola! Muy buena publicación, me gustaría que me ayudes con un problema más didáctico, más fácil de entender, que incluya todos los procesos que publicaste.
Muchas Gracias
Luis Salcedo Deja una respuesta
Excelente !