Implementación de un Árbol AVL - Estructuras de Datos con Python
Introducción:
Hola amigos de Internet, les doy la bienvenida a Mi Diario Python, el mejor blog para Aprender Python.
En este articulo, nos enfocaremos en conocer los principios básicos de los árboles AVL, un tipo especial de árbol binario. Al final, realizaremos una implementación utilizando el lenguaje de programación Python.
¿Que es un árbol AVL?
Los árboles AVL son un tipo especial de árbol binario. Inventado por los matemáticos rusos Adelson-Velskii y Landis, de allí el nombre AVL.
El árbol AVL tiene la peculiaridad de ser el primer árbol binario auto-balanceable.
Los árboles AVL están siempre equilibrados de tal modo que para todos los nodos la altura de la rama izquierda no difiere en más de una unidad de la altura de la rama derecha o viceversa.
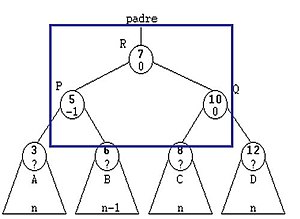
La siguiente imagen es una representación de su equilibrio:
Para conseguir esta propiedad de equilibrio, la inserción y borrado de los nodos se ha de realizar de una forma especial. Si al realizar una operación de inserción o borrado de rompe la condición de equilibrio, hay que realizar una serie de rotaciones de nodos.
Representación de una construcción de un árbol AVL y sus rotaciones
Operaciones:
Otro punto a tener en cuenta son las operaciones que se pueden realizar en un árbol AVL. Esto nos servira para saber que métodos agregar al momento de la implementación.
Rotaciones:
El reequilibrado se produce de abajo hacia arriba sobre los nodos en los que se produce el desequilibrio. Pueden darse dos casos: rotación simple o rotación doble; a su vez ambos casos pueden ser hacia la derecha o hacia la izquierda.
Podemos realizar 4 tipos de rotaciones:
Rotación simple a la derecha:
De un árbol de raíz (r) y de hijos izquierdo (i) y derecho (d), lo que haremos será formar un nuevo árbol cuya raíz sea la raíz del hijo izquierdo, como hijo izquierdo colocamos el hijo izquierdo de i (nuestro i’) y como hijo derecho construimos un nuevo árbol que tendrá como raíz, la raíz del árbol (r), el hijo derecho de i (d’) será el hijo izquierdo y el hijo derecho será el hijo derecho del árbol (d).
Rotación simple a la izquierda:
De un árbol de raíz (r) y de hijos izquierdo (i) y derecho (d), consiste en formar un nuevo árbol cuya raíz sea la raíz del hijo derecho, como hijo derecho colocamos el hijo derecho de d (nuestro d’) y como hijo izquierdo construimos un nuevo árbol que tendrá como raíz la raíz del árbol (r), el hijo izquierdo de d será el hijo derecho (i’) de r y el hijo izquierdo será el hijo izquierdo del árbol (i).
Precondición : Tiene que tener hijo derecho no vacío.
Rotación doble a la derecha:
La Rotación doble a la Derecha son dos rotaciones simples, primero rotación simple izquierda y luego rotación simple derecha.
Rotación doble a la izquierda
La Rotación doble a la Izquierda son dos rotaciones simples, primero rotación simple derecha y luego rotación simple izquierda.
Inserción:
La inserción en un árbol de AVL puede ser realizada insertando el valor dado en el árbol como si fuera un árbol de búsqueda binario desequilibrado y después retrocediendo hacia la raíz, rotando sobre cualquier nodo que pueda haberse desequilibrado durante la inserción.
Proceso de inserción:
- Buscar hasta encontrar la posición de inserción o modificación (proceso idéntico a inserción en árbol binario de búsqueda).
- Insertar el nuevo nodo con factor de equilibrio “equilibrado”.
- Desandar el camino de búsqueda, verificando el equilibrio de los nodos, y re-equilibrando si es necesario.
Referencias:
Implementación:
Ahora sí es el momento de escribir código.
""" Árbol AVL - Implementación en Python """ from __future__ import print_function """ Declaramos la clase "Node", con cada una de sus propiedades. """ class Node: def __init__(self, label): self.label = label self._parent = None self._left = None self._right = None self.height = 0 @property def right(self): return self._right @right.setter def right(self, node): if node is not None: node._parent = self self._right = node @property def left(self): return self._left @left.setter def left(self, node): if node is not None: node._parent = self self._left = node @property def parent(self): return self._parent @parent.setter def parent(self, node): if node is not None: self._parent = node self.height = self.parent.height + 1 else: self.height = 0 # Declaramos la clase AVL class AVL: def __init__(self): self.root = None self.size = 0 """ Operación de inserción para agregar nuevos nodos al árbol. """ def insert(self, value): node = Node(value) if self.root is None: self.root = node self.root.height = 0 self.size = 1 else: dad_node = None curr_node = self.root while True: if curr_node is not None: dad_node = curr_node if node.label < curr_node.label: curr_node = curr_node.left else: curr_node = curr_node.right else: node.height = dad_node.height dad_node.height += 1 if node.label < dad_node.label: dad_node.left = node else: dad_node.right = node self.rebalance(node) self.size += 1 break # Operación de rotación def rebalance(self, node): n = node while n is not None: height_right = n.height height_left = n.height if n.right is not None: height_right = n.right.height if n.left is not None: height_left = n.left.height if abs(height_left - height_right) > 1: if height_left > height_right: left_child = n.left if left_child is not None: h_right = (left_child.right.height if (left_child.right is not None) else 0) h_left = (left_child.left.height if (left_child.left is not None) else 0) if (h_left > h_right): self.rotate_left(n) break else: self.double_rotate_right(n) break else: right_child = n.right if right_child is not None: h_right = (right_child.right.height if (right_child.right is not None) else 0) h_left = (right_child.left.height if (right_child.left is not None) else 0) if (h_left > h_right): self.double_rotate_left(n) break else: self.rotate_right(n) break n = n.parent def rotate_left(self, node): aux = node.parent.label node.parent.label = node.label node.parent.right = Node(aux) node.parent.right.height = node.parent.height + 1 node.parent.left = node.right def rotate_right(self, node): aux = node.parent.label node.parent.label = node.label node.parent.left = Node(aux) node.parent.left.height = node.parent.height + 1 node.parent.right = node.right def double_rotate_left(self, node): self.rotate_right(node.getRight().getRight()) self.rotate_left(node) def double_rotate_right(self, node): self.rotate_left(node.getLeft().getLeft()) self.rotate_right(node) def empty(self): if self.root is None: return True return False def preShow(self, curr_node): if curr_node is not None: self.preShow(curr_node.left) print(curr_node.label, end=" ") self.preShow(curr_node.right) def preorder(self, curr_node): if curr_node is not None: self.preShow(curr_node.left) self.preShow(curr_node.right) print(curr_node.label, end=" ") def getRoot(self): return self.root if __name__ == '__main__': t = AVL() t.insert(5) t.insert(9) t.insert(13) t.insert(10) t.insert(17) t.preShow(t.root)
5 9 10 13 17
El método preShow nos mostrara nos nodos del árbol. Todo de manera equilibrada.
¿Alguna duda? No dudes en dejar tu comentario.
Mi nombre es Luis, y fue un placer compartir mis conocimientos con todos ustedes :D.
Deja una respuesta
Se podrá aplicar éste programa para gramática para el esquema arbóreo.