Mi Diario Python

Operaciones con Polinomios en Python

PythonDiario

22/09/2017 - Actualizado: 22/12/2020


Introducción:

En este articulo te mostrare como hacer operaciones con polinomios, con el lenguaje de programación Python y utilizando la librería Sympy que nos permite trabajar con matemática simbólica, crearemos un programa que tome como entrada, dos polinomios, luego el programa realizara operaciones aritméticas entre estos Polinomios, y retornara un resultado. 
Pero antes de empezar con el programa, vamos a ver que es un Polinomio.

Artículo escrito por Luis Salcedo
GitHub: algoritmosmathpy

¿Que es un Polinomio?

Un polinomio es una expresión algebraica que se obtiene al sumar dos o más monomios. A cada monomio se le llama término del polinomio. Si tiene dos términos se llama binomio; si tiene tres trinomio, etc.
Ahora te mostrare algunos ejemplos:
Índice

Adición de polinomios:

La suma de polinomios es una operación en la que partiendo de dos polinomios P(x) y Q(x), obtenemos un tercero R(x).
Ejemplo: Adición de polinomios.
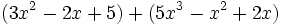
(3x^2 - 2x + 5 ) + ( 5x^3 - x^2 + 2x ) ;!
Resultado:
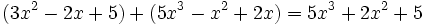
(3x^2 - 2x + 5 ) + ( 5x^3 - x^2 + 2x ) = 5x^3+2x^2+5 ;!

Sustracción de polinomios:

Si podemos sumar, tambien podemos restar, veamos un ejemplo:
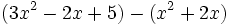
(3x^2 - 2x + 5 ) - ( x^2 + 2x) ;!
El resultado seria el siguiente:
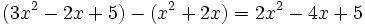
(3x^2 - 2x + 5 ) - (x^2 + 2x ) = 2x^2-4x+5 ;!

Multiplicación de dos polinomios:

Ya vimos como sumar polinomios, pero ahora vamos a multiplicar un polinomio por otro polinomio, veamos un  ejemplo.
Tenemos los siguientes polinomios a los cuales calcularemos el producto:
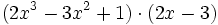
(2x^3 - 3x^2 +1) cdot (2x-3);!
El resultado seria el siguiente:
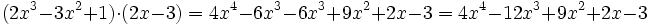
(2x^3 - 3x^2 +1) cdot (2x-3) = 4x^4-6x^3-6x^3+9x^2+2x-3=4x^4-12x^3+9x^2+2x-3 ;!

División de polinomios:

La división de polinomios tiene las mismas partes que la división aritmética, así hay dos polinomios P(x) (dividendo) y Q(x) (divisor) de modo que el grado de P(x) sea mayor que el grado de Q(x) y el grado de Q(x) sea mayor o igual a cero. Ejemplo:


El poder de Sympy:

Ahora que conocemos mejor a los polinomios, ya podes crear nuestro programa para que nos ayude a resolver operaciones con polinomios.
Para la creación del programa de hoy, usaremos una librería muy buena, que nos permite trabajar con matemática simbólica, se trata de Sympy, puedes descargar la librería sympy desde el siguiente enlace, https://pypi.python.org/pypi/sympy.
Comencemos nuestro programa paso a paso.

Resolvedor de Polinomios:

"Resolvedor de Polinomios" sera el nombre de nuestro programa.
Al iniciar, el programa le pedirá al usuario que introduzca los dos polinomios, en este caso yo usare como ejemplo los siguiente polinomios.
P(x) = 7*x**3 + 2*x**2 + x - 7
Q(x) = x**2 + 3
Luego convertiremos esta entrada a un polinomio, esto lo haremos con  la función "Poly" de "Sympy", luego de que el programa haga una conversión de la entrada en algo que entiende, definiremos una función para cada operación arimetica que queramos hacer, y por ultimo mostraremos el resultado deseado.
Empecemos:

Paso 1: Importamos las librerías necesarias.

-Una vez ya instalada la librería sympy, la importamos en nuestro script.
#Importamos Sympy
import sympy

Paso 2: Pedimos los 2 polinomios como entrada.

#Obtenes los dos polinomios introducidos por el usuario
P1 = input("Primer Polinomio: ")
P2 = input("Segundo Polinomio: ")
print("n")

Paso 3: Definimos los simbolos que usaremos (x,y).

#Definimos los simbolos con la funcion symbols de sympy
sympy.init_printing()
x,y = sympy.symbols('x,y')

Paso 4: Hacer la conversión de la entrada a polinomios y declaración de funciones.

#Luego almacenamos en variables los dos polinomios procesados por la función Poly de sympy Poly1 = sympy.Poly(P1)
Poly2 = sympy.Poly(P2)
#Declaramos una función para cada operación que queramos utilizar
def mult(p1, p2):
    return p1 * p2
def suma(p1, p2):
    return p1 + p2
def res(p1, p2):
    return p1 - p2
def div(p1, p2):
    return p1 / p2

Paso 5: Mostramos el resultado.

-Imprimimos el resultado llamando a la función deseada, depende de que operación quieres realizar, y pasamos como parámetro a los dos polinomios.

#Mostramos el valor que deseemos
print("Resultado: ", mult(Poly1, Poly2))

Ejecución del Programa:

-Puedes probar el programa desde tu terminal.
Si quieres ver el codigo completo puedes entrar en mi repositorio de github: https://github.com/algoritmosmathpy/algoritmos-python/blob/master/Operaciones%20entre%20dos%20Polinomios.py

Finalización:

Hemos llegado al final, te dejo como tarea encontrar el resultado de una multiplicación entre los siguientes polinomios: (Deja tu respuesta en los comentarios)

P(x) = 7*x**3 + 2*x**2 + x - 7
Q(x) = x**2 + 3
Así podrás verificar si el programa funciona correctamente. 😀

PythonDiario

  1. Ron dice:
    septiembre 23, 2017 a las 2:53 am

    Resultado: Poly(7*x**5 + 2*x**4 + 22*x**3 - x**2 + 3*x - 21, x, domain='ZZ')

    Responder
    1. Luis Salcedo dice:
      septiembre 23, 2017 a las 2:06 pm

      Excelente, respuesta correcta 😀

      Responder
  2. Miguel López dice:
    septiembre 23, 2017 a las 12:12 pm

    Muy útil realmente genial.

    Responder
    1. Luis Salcedo dice:
      septiembre 23, 2017 a las 2:07 pm

      Sí, esto nos sera muy útil al momento de hacer la tarea de matemática. 😀

      Responder
  3. FonsiHer dice:
    noviembre 18, 2019 a las 1:21 am

    Sirve solo en las versiones más actuales de Python o en qué versión te funciona ?

    Responder
  4. Unknown dice:
    mayo 6, 2020 a las 3:00 am

    No funciona la division de polinomios de manera correcta.

    Responder
  5. Unknown dice:
    septiembre 2, 2020 a las 10:10 pm

    Hola! Me pueden ayudar con el sig ejercicio?
    Evalua el polinomio (x4+ 10x3 + 1/2x2 -x) en ×= 3.1 y almacena el resultado en la variable y
    Luego modifica el valor de x por -6.6 y evalua nuevamente el polinomio. Almacena el resultado en la variable z
    Por último almacena en la variable redondeo el resultado de redondear a un valor entero el valor de z (utilizar la función round)
    Utiliza variables para x,y,z y redondeo

    Responder
  6. Unknown dice:
    septiembre 2, 2020 a las 10:15 pm

    Hola! Me pueden ayudar con el sig ejercicio?
    Evalua el polinomio (x4+ 10x3 + 1/2x2 -x) en ×= 3.1 y almacena el resultado en la variable y
    Luego modifica el valor de x por -6.6 y evalua nuevamente el polinomio. Almacena el resultado en la variable z
    Por último almacena en la variable redondeo el resultado de redondear a un valor entero el valor de z (utilizar la función round)
    Utiliza variables para x,y,z y redondeo

    Responder
  7. Anónimo dice:
    septiembre 2, 2020 a las 10:16 pm

    Hola! Me pueden ayudar con el sig ejercicio?
    Evalua el polinomio (x4+ 10x3 + 1/2x2 -x) en ×= 3.1 y almacena el resultado en la variable y
    Luego modifica el valor de x por -6.6 y evalua nuevamente el polinomio. Almacena el resultado en la variable z
    Por último almacena en la variable redondeo el resultado de redondear a un valor entero el valor de z (utilizar la función round)
    Utiliza variables para x,y,z y redondeo

    Responder

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Subir
White Monkey